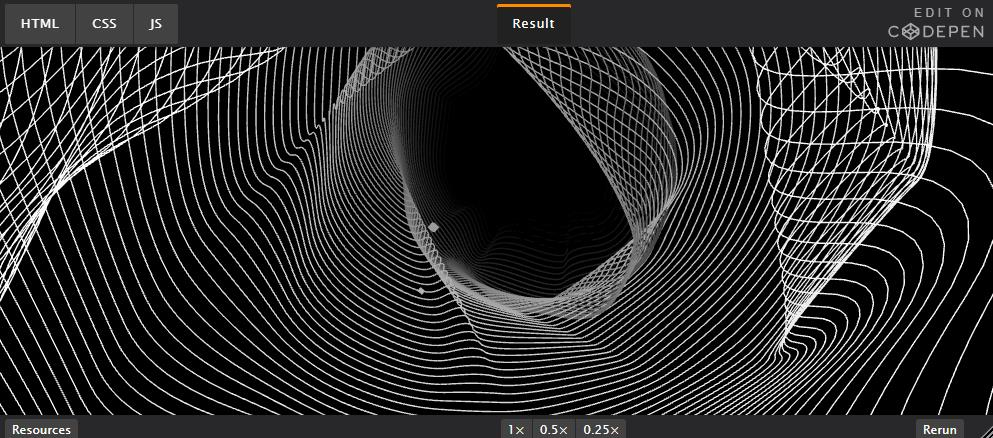
除了優(yōu)雅之外，貝塞爾曲線還因其定義和構(gòu)造而具有良好的數(shù)學(xué)特性。難怪它們被廣泛應(yīng)用于這么多領(lǐng)域：
· 作為繪圖/設(shè)計(jì)工具：它們?cè)谑噶坷L圖軟件中通常被稱為“路徑”。
· 作為表示曲線的格式：它們用于 SVG、字體和許多其他矢量圖形格式。
· 作為數(shù)學(xué)函數(shù)：通常用于控制動(dòng)畫時(shí)間。
現(xiàn)在，如何使用貝塞爾曲線作為 CSS 的運(yùn)動(dòng)路徑？
 

快速回顧

根據(jù)上下文，當(dāng)提到“貝塞爾曲線”時(shí)，我們通常假設(shè)是二維三次貝塞爾曲線。
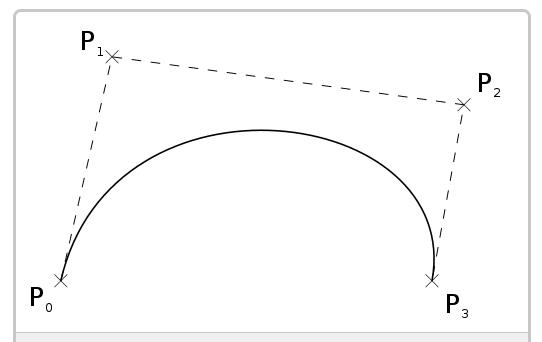
這樣的曲線由四個(gè)點(diǎn)定義：
“三次”一詞表示曲線的基礎(chǔ)函數(shù)是三次多項(xiàng)式。還有類似的“二次”貝塞爾曲線，但控制點(diǎn)少了一個(gè)。

問(wèn)題

假設(shè)給定了一條任意的 2D 三次 Beizer 曲線，您將如何使用純 CSS 動(dòng)畫為元素設(shè)置動(dòng)畫，使其  沿著曲線精確移動(dòng)？
例如，您將如何重新創(chuàng)建此動(dòng)畫？



在本文中，我們將探索三種不同風(fēng)格的方法。對(duì)于每個(gè)解決方案，我們將展示一個(gè)交互式演示，然后解釋它是如何工作的。幕后有很多數(shù)學(xué)計(jì)算和證明，但請(qǐng)放心，我們不會(huì)講得很深。
開始吧！

方法一：時(shí)間扭曲

這是基本的想法：

• 設(shè)置@keyframes以將元素從曲線的一個(gè)端點(diǎn)移動(dòng)到另一個(gè)端點(diǎn)。
• 分別扭曲每個(gè)坐標(biāo)的時(shí)間，使用animation-timing-function.

使用cubic-bezier()具有正確參數(shù)的函數(shù)，我們可以創(chuàng)建任何三次貝塞爾曲線的運(yùn)動(dòng)路徑：



這個(gè)演示展示了一個(gè)純 CSS 動(dòng)畫。然而使用了 canvas 和 JavaScript，它們有兩個(gè)目的：

• 可視化底層貝塞爾曲線（紅色曲線）。
• 允許使用典型的“路徑”UI 調(diào)整曲線。

您可以拖動(dòng)兩個(gè)端點(diǎn)（黑點(diǎn)）和兩個(gè)控制點(diǎn)（黑色方塊）。JavaScript 代碼將通過(guò)更新一些 CSS 變量相應(yīng)地更新動(dòng)畫。

這個(gè)怎么運(yùn)作


 

假設(shè)所需的三次貝塞爾曲線由四個(gè)點(diǎn)定義：p0、p1、p2和p3。我們?cè)O(shè)置 CSS 規(guī)則如下：
規(guī)則并確定元素的開始和結(jié)束位置@keyframes。在我們有兩個(gè)神奇的 函數(shù)中，參數(shù)的計(jì)算使得兩者在任何時(shí)候都始終具有正確的值。move-xmove-yanimation-timing-functioncubic-bezier()topleft
我會(huì)跳過(guò)數(shù)學(xué)，但我在這里起草了一個(gè)簡(jiǎn)短的證明，供你好奇的數(shù)學(xué)頭腦使用。

討論

這種方法應(yīng)該適用于大多數(shù)情況。您甚至可以通過(guò)為該值引入另一個(gè)動(dòng)畫來(lái)制作 3D 三次貝塞爾曲線 z 。
但是，有一些小警告：

• 由于被零除錯(cuò)誤，當(dāng)兩個(gè)端點(diǎn)位于水平或垂直線上時(shí)，它不起作用。

• 它不支持階數(shù)高于 的貝塞爾曲線 3。
• 動(dòng)畫時(shí)間選項(xiàng)有限。
  • 我們使用 1/3 和 2/3 以上來(lái)實(shí)現(xiàn)線性時(shí)序。
  • 您可以調(diào)整這兩個(gè)值來(lái)調(diào)整時(shí)間，但與其他方法相比它是有限的。稍后會(huì)詳細(xì)介紹。

方法二：標(biāo)準(zhǔn)貝塞爾曲線構(gòu)造

貝塞爾曲線的數(shù)學(xué)構(gòu)造已經(jīng)給了我們很好的提示。




一步一步，我們可以確定所有移動(dòng)點(diǎn)的坐標(biāo)。p0首先，我們確定在和之間移動(dòng)的綠點(diǎn)的位置p1：



可以用類似的方式構(gòu)建額外的綠點(diǎn)。
接下來(lái)，我們可以像這樣確定藍(lán)點(diǎn)的位置：



沖洗并重復(fù)，最終我們會(huì)得到想要的曲線。



 

結(jié)論

在本文中，我們討論了 2 種僅使用 CSS 動(dòng)畫沿著貝塞爾曲線精確移動(dòng)元素的不同方法。
雖然所有 2 種方法都或多或少實(shí)用，但它們各有利弊：

• 方法 1 對(duì)于熟悉計(jì)時(shí)函數(shù) hack 的人來(lái)說(shuō)可能更直觀。但是它在動(dòng)畫時(shí)間方面不太靈活。
• 對(duì)于熟悉貝塞爾曲線數(shù)學(xué)構(gòu)造的人來(lái)說(shuō)，方法 2 更有意義。動(dòng)畫時(shí)間也很靈活。另一方面，由于使用@property.

就這樣！我希望你覺(jué)得這篇文章很有趣。請(qǐng)讓我知道你的想法！